Image Processing 10. Convolution Kernel

With convolution kernel it's possible to implement numerous interesting effects, such as motion blur, sharpening, edge detecting, emboss, etc. These effects we going to explore in this article.

If we modify the previous blur effect example with a radius 1 (i.e., examining 3×3 pixels) so that each color component from the 9 sampled pixels is multiplied by corresponding coefficients, summed, and then divided by some value – we get convolution.

To make it more universal, we introduce an offset parameter alongside the 3×3 coefficient array (called the convolution kernel) and divisor div The offset is added to each color component, allowing brightness adjustment.

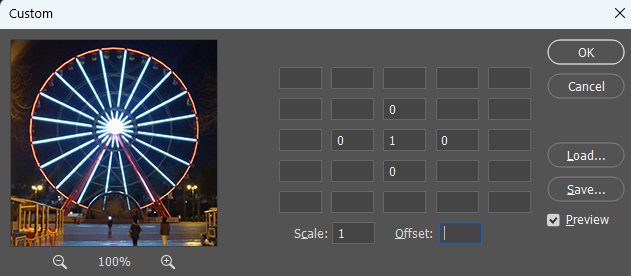
Of course, kernels aren't limited to 3×3, you can have 5×5 or even larger kernels. Photoshop uses 5×5 kernels under Filter → Other → Custom.

const kernelSize = 3;
const halfSize = Math.floor(kernelSize / 2);
let kernel = [/* 3x3 */];
let div = 1;
let offset = 0;

let dstIndex = 0;
for (let y = 0; y < height; y++) {
  for (let x = 0; x < width; x++) {
    let r = 0, g = 0, b = 0;
    for (let sy = 0; sy < kernelSize; sy++) {
      const yy = Math.min(height - 1, Math.max(0, y + sy - halfSize));
      for (let sx = 0; sx < kernelSize; sx++) {
        const xx = Math.min(width - 1, Math.max(0, x + sx - halfSize));
        let pix = src[yy * width + xx];
        r += (pix & 0xFF) * kernel[sy][sx];
        g += ((pix >> 8) & 0xFF) * kernel[sy][sx];
        b += ((pix >> 16) & 0xFF) * kernel[sy][sx];
      }
    }
    
    const a = src[y * width + x] & 0xFF000000;
    r = Math.min(255, Math.max(0, offset + (r / div))) & 0xFF;
    g = Math.min(255, Math.max(0, offset + (g / div))) & 0xFF;
    b = Math.min(255, Math.max(0, offset + (b / div))) & 0xFF;
    
    dst[dstIndex++] = a | (b << 16) | (g << 8) | r;
  }
}

By default, the kernel is defined as:

0 0 0
0 1 0
0 0 0
div: 1, offset: 0

This means that only the current pixel is considered, while all surrounding pixels are multiplied by zero. As a result, we get an image without changes.

1 1 1
1 1 1
1 1 1
div: 9, offset: 0

Here, all 9 pixels are summed and divided by 9. This recreates the blur effect from the previous article using convolution kernel.

1 2 1
2 4 2
1 2 1
div: 16, offset: 0

The same blur effect, but now with coefficients weighted by distance from the center. This is an approximate Gaussian blur.

 0 -1  0
-1  5 -1
 0 -1  0
div: 1, offset: 0

If a negative coefficient is specified in the kernel, it means it'll be subtracted from the sum. If you subtract the values of 4 surrounding pixels, but give the center pixel 5 times the strength, you get a Sharpening effect.

Reducing coefficients softens the sharpening effect.

  0   -0.2    0
-0.2   1.8  -0.2
  0   -0.2    0
div: 1, offset: 0

-2 -1  0
-1  1  1
 0  1  2
div: 1, offset: 0

A diagonal Emboss effect. Kernels can be transposed for vertical/horizontal variations.

-2 -1  0
-1  0  1
 0  1  2
div: 1, offset: 0

Ignoring the central pixel gives us an Edge Detection effect.

Setting offset=128 produces a Relief effect:

-2 -1  0
-1  0  1
 0  1  2
div: 1, offset: 128

Convolution kernel can also negate images:

0  0  0
0 -1  0
0  0  0
div: 1, offset: 255

For an interactive visualization of convolution kernels and their summed effects but on grayscale images, visit https://setosa.io/ev/image-kernels/